UNIVERSIDAD TÉCNICA PARTICULAR DE LOJA
MATEMÁTICAS
FUNCIONES
Que es un función?
En matemáticas, se dice que una magnitud o cantidad es función de otra si el valor de la primera depende exclusivamente del valor de la segunda. Por ejemplo el área A de un círculo es función de su radio r: el valor del área es proporcional al cuadrado del radio, A = π·r2. Del mismo modo, la duración T de un viaje de tren entre dos ciudades separadas por una distancia d de 150 km depende de la velocidad v a la que este se desplace: la duración es inversamente proporcional a la velocidad, d / v. A la primera magnitud (el área, la duración) se la denomina variable dependiente, y la cantidad de la que depende (el radio, la velocidad) es la variable independiente.
En análisis matemático, el concepto general de función, aplicación se refiere a una regla que asigna a cada elemento de un primer conjunto un único elemento de un segundo conjunto (correspondencia matemática). Por ejemplo, cada número entero posee un único cuadrado, que resulta ser un número natural (incluyendo el cero)
FUNCIONES LINEALES
Las ecuaciones lineales contienen una o dos variables. La palabra "lineal" proviene del hecho de que la gráfica de la ecuación es una línea recta. Por ejemplo: x + y = 10 es una ecuación lineal con dos variables: x e y. Una variable, en oposición a una constante, puede tomar valores diferentes, dependiendo de la ecuación.
APLICACIÓN
DE LAS FUNCIONES LINEALES
FUNCIONES EXPONENCIALES
La función exponencial, es
conocida formalmente como la función real ex,
donde e es el número de Euler aproximadamente
2.71828...; esta función tiene por dominio
de definición el conjunto de los números reales, y tiene la
particularidad de que suderivada es la misma función. Se denota
equivalentemente como f(x)=ex o exp(x), donde e es
la base de los logaritmos naturales y corresponde a la función inversa del logaritmo
natural.
En
términos mucho más generales, una función real E(x) se dice que es del tipo exponencial en base a si tiene la forma
siendo a, K ∈ R números reales con a > 0. Así pues, se obtiene un
abanico de exponenciales, todas ellas similares, que dependen de la base a que utilicen.
Funciones Logaritmicas
Los logaritmos fueron introducidos por John Napier a principios del siglo XVII como un medio de simplificación de los cálculos. Estos fueron prontamente adoptados por científicos, ingenieros, banqueros y otros para realizar operaciones fácil y rápidamente, usando reglas de cálculo y tablas de logaritmos. Estos dispositivos se basan en el hecho más importante — por identidades logarítmicas — que el logaritmo de un producto es la suma de los logaritmos de los factores:
Funciones Trigonométricas
Las Razones trigonométricas se definen comúnmente como el cociente entre dos lados de un triángulo rectángulo asociado a sus ángulos. Las funciones trigonométricas son funciones cuyos valores son extensiones del concepto de razón trigonométrica en un triángulo rectángulo trazado en una circunferencia unitaria (de radio unidad). Definiciones más modernas las describen como series infinitas o como la solución de ciertas ecuaciones diferenciales, permitiendo su extensión a valores positivos y negativos, e incluso a números complejos.
Existen seis funciones trigonométricas básicas. Las últimas cuatro, se definen en relación de las dos primeras funciones, aunque se pueden definir geométrica mente o por medio de sus relaciones.



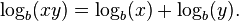
.jpg)






.jpg)

.jpg)

.jpg)




