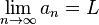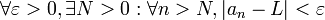LIMITES Y CONTINUIDAD

La definición de límite matemático para el caso de una sucesión nos indica intuitivamente que los términos de la sucesión se aproximan arbitrariamente a un único número o punto , si existe, para valores grandes de . Esta definición es muy parecida a la definición dellímite de una función cuando  tiende a .

Formalmente, se dice que la sucesión  tiende hasta su límite , o que converge o es convergente (a ), y se denota como:

si y solo si para todo valor real ε>0 se puede encontrar un número natural  tal que todos los términos de la sucesión, a partir de un cierto valor natural  mayor que  converjan a  cuando  crezca sin cota. Escrito en un lenguaje formal, y de manera compacta:

 

Este límite, si existe, se puede demostrar que es único. Si los términos de la sucesión no convergen a ningún punto específico, entonces se dice que la sucesión es divergente.

Propiedades de los limites 

Límite de una suma

Límite de un producto

Límite de un cociente

Límite de una potencia

Límite de una función

g puede ser una raíz, un log, sen ,cos, tg, etc.

Límite de una raíz

Límite de un logaritmo

Limite de un polinomio

P(x) = a_nxⁿ + a_n-1x^n-1 + ... + a₁x + a₀

1) lim_x->b P(x) = P(b)

Ejemplo: lim_x->1 x² + 2x - 1 = 2

2) lim_x->inf P(x) = lim_x->inf a_nxⁿ

lim_x->inf P(x) =lim_x->inf a_nxⁿ+a_n-1x^n-1+...+a₁x+a₀
a_nxⁿ (1+a_n-1 +a_n-2 +...+ a₁ + a₀) = lim a_nxⁿ

=lim   ---    ---        ---     ---    x->inf

x->inf       a_nx    a_nx²       a_nx^n-1  a_nxⁿ

Limite de una función racional

una función racional de una variable es una función que puede ser expresada de la forma:

donde P y Q son polinomios y x una variable, siendo Q distinto del polinomio nulo. Las funciones racionales están definidas o tienen sudominio de definición en todos los valores de x que no anulen el denominador.¹ Obviamente esta definición puede extenderse a un número finito pero arbitrario de variables, usando polinimios de varias variables.

La palabra "racional" hace referencia a que la función racional es una razón o cociente (de dos polinomios); los coeficientes de los polinomios pueden ser números racionales o no.

Limite de una funcion compuesta:

 una función compuesta es una función formada por la composición o aplicación sucesiva de otras dos funciones. Para ello, se aplica sobre el argumento la función más próxima al mismo, y al resultado del cálculo anterior se le aplica finalmente la función restante.

Usando la notación matemática, la función compuesta g ∘ f: X → Z expresa que (g ∘ f)(x) = g(f(x)) para todo x perteneciente X.

A g ∘ f se le llama composición de f y g. Nótese que se nombra no siguiendo el orden de escritura, sino el orden en que se aplican las funciones a su argumento.

De manera formal, dadas dos funciones f: X → Y y g: Y → Z, donde la imagen de f está contenida en el dominio de g, se define la función composición (g ∘ f ): X → Z como (g ∘ f)(x) = g (f(x)), para todos los elementos de X.

También se puede representar de manera gráfica usando la categoría de conjuntos, mediante un diagrama conmutativo:

Funciones trigonometricas

las funciones trigonométricas son las funciones establecidas con el fin de extender la definición de las razones trigonométricas a todos los números reales y complejos.

Las funciones trigonométricas son de gran importancia en física, astronomía, cartografía, náutica, telecomunicaciones, la representación de fenómenos periódicos, y otras muchas aplicaciones.

 f(x) = sen x

Dominio: 

Recorrido: [−1, 1]

Período: 

Continuidad: Continua en 

Creciente en: 

Decreciente en: 

Máximos: 

Mínimos: 

Impar: sen(−x) = −sen x

Cortes con el eje OX: 

Limites infinitos

Observemos la función f(x)=1/x² para valores de x positivos muy grandes.

x	f(x)
100	1,0x10-4
1.000	1,0x10-6
10.000	1,0x10-8
100.000	1,0x10-10
1.000.000	1,0x10-12

Si tomamos x cada vez mayor, f(x) está cada vez más cerca de 0. Si x es suficientemente grande podemos conseguir que f(x) se acerque a 0 tanto como queramos. Decimos que f(x) tiende a 0 cuando x tiende a infinito.

Continuidad de una funcion

Una función continua es aquella para la cual, intuitivamente, 

para puntos cercanos del dominio se producen pequeñas variaciones    
en los valores de la función. Si la función no es continua, se dice  
que es discontinua. Una función continua de  en  es aquella 
cuya gráfica puede dibujarse sin levantar el lápiz del papel (más 
formalmente sugrafo es un conjunto conexo).La continuidad de funciones 
es uno de los conceptos principales del análisis matemático y de la topología. 
El artículo describe principalmente la continuidad de funciones reales de una
 variable real.