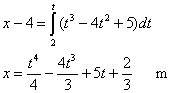APLICACIÓN DE LAS DERIVADAS
EN LA ARQUITECTURA
DEFINICIÓN:
La derivada de una función es un concepto local, es decir, se calcula
como el Limite de
la rapidez de cambio media de la función en un cierto intervalo, cuando el
intervalo considerado para la variable independiente se torna cada vez más
pequeño. Por ello se habla del valor de la derivada de una cierta función en
un punto dado.
La derivada de una función f en un punto x se
denota como f′(x). La función cuyo
valor en cada punto x es esta derivada es la llamada
función derivada de f, denotada por f′. El proceso de
encontrar la derivada de una función se denomina diferenciación, y es
una de las herramientas principales en el área de las matemáticas conocida como calculo infinitesimal. Correctamente el que trata de asuntos
vinculados con la derivada se denomina cálculo diferencial.
REGLAS DE LAS DERIVADAS
EJERCICIOS:
REGLA DE LA CADENA
En términos intuitivos, si una variable y, depende de una segunda variable u, que a la vez depende de una tercera variable x; entonces, la razón de cambio de y con respecto a x puede ser calculada con el producto de la razón de cambio de y con respecto a u multiplicado por la razón de cambio de u con respecto a x.
En términos alg, la algebraicos, la de la cadena (para funciones de una variable) afirma que si  es diferenciable en
es diferenciable en  y
y  es una función diferenciable en
es una función diferenciable en  , entonces la función compuesta
, entonces la función compuesta 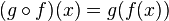 es diferenciable en
es diferenciable en  y
y
 es diferenciable en
es diferenciable en  y
y  es una función diferenciable en
es una función diferenciable en  , entonces la función compuesta
, entonces la función compuesta 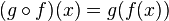 es diferenciable en
es diferenciable en  y
y
MOVIMIENTO RECTILÍNEO
Se denomina movimiento rectilíneo, aquél cuya trayectoria es una línea recta.
En la recta situamos un origen O, donde estará un observador que medirá la posición del móvil x en el instante t. Las posiciones serán positivas si el móvil está a la derecha del origen y negativas si está a la izquierda del origen.
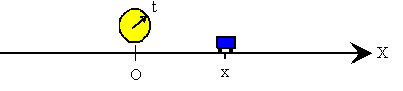
Posición
La posición x del móvil se puede relacionar con el tiempo t mediante una función x=f(t).
Desplazamiento
Supongamos ahora que en el tiempo t, el móvil se encuentra en posición x, más tarde, en el instante t' el móvil se encontrará en la posición x'. Decimos que móvil se ha desplazado Dx=x'-x en el intervalo de tiempo Dt=t'-t, medido desde el instante t al instante t'.
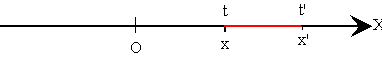
Velocidad
La velocidad media entre los instantes t y t' está definida por
Para determinar la velocidad en el instante t, debemos hacer el intervalo de tiempo Dt tan pequeño como sea posible, en el límite cuando Dt tiende a cero.
Pero dicho límite, es la definición de derivada de x con respecto del tiempo t.
Para comprender mejor el concepto de velocidad media, resolvemos el siguiente ejercicio
Ejercicio:
Una partícula se mueve a lo largo del eje X, de manera que su posición en cualquier instante t está dada por x=5·t2+1, donde x se expresa en metros y t en segundos.
Calcular su velocidad promedio en el intervalo de tiempo entre:
- 2 y 3 s.
- 2 y 2.1 s.
- 2 y 2.01 s.
- 2 y 2.001 s.
- 2 y 2.0001 s.
- Calcula la velocidad en el instante t=2 s.
En el instante t=2 s, x=21 m
| ||||
t’ (s)
|
x’ (m)
|
Δx=x'-x
|
Δt=t'-t
| |
3
|
46
|
25
|
1
|
25
|
2.1
|
23.05
|
2.05
|
0.1
|
20.5
|
2.01
|
21.2005
|
0.2005
|
0.01
|
20.05
|
2.001
|
21.020005
|
0.020005
|
0.001
|
20.005
|
2.0001
|
21.00200005
|
0.00200005
|
0.0001
|
20.0005
|
...
|
...
|
...
|
...
|
...
|
0
|
20
| |||
Como podemos apreciar en la tabla, cuando el intervalo Δt→0, la velocidad media tiende a 20 m/s. La velocidad en el instante t=2 s es una velocidad media calculada en un intervalo de tiempo que tiende a cero.
Calculamos la velocidad en cualquier instante t
- La posición del móvil en el instante t es x=5t2+1
- La posición del móvil en el instante t+Dt es x'=5(t+Dt)2+1=5t2+10tDt+5Dt2+1
- El desplazamiento es Dx=x'-x=10tDt+5Dt2
- La velocidad media <v> es
La velocidad en el instante t es el límite de la velocidad media cuando el intervalo de tiempo tiende a cero
La velocidad en un instante t se puede calcular directamente, hallando la derivada de la posición x respecto del tiempo.
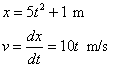
En el instante t=2 s, v=20 m/s
Aceleración
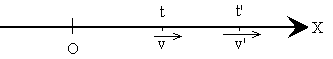
En general, la velocidad de un cuerpo es una función del tiempo. Supongamos que en un instante t la velocidad del móvil es v, y en el instante t' la velocidad del móvil es v'. Se denomina aceleración media entre los instantes t y t' al cociente entre el cambio de velocidad Dv=v'-v y el intervalo de tiempo en el que se ha tardado en efectuar dicho cambio, Dt=t'-t.
La aceleración en el instante t es el límite de la aceleración media cuando el intervalo Dt tiende a cero, que es la definición de la derivada de v.
Ejemplo:
Un cuerpo se mueve a lo largo de una línea recta x=2t3-4t2+5 m. Hallar la expresión de
- La velocidad
- La aceleración del móvil en función del tiempo.
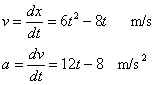
Dada la velocidad del móvil hallar el desplazamiento:
Si conocemos un registro de la velocidad podemos calcular el desplazamiento x-x0 del móvil entre los instantes t0 y t, mediante la integral definida.
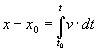
El producto v dt representa el desplazamiento del móvil entre los instantes t y t+dt, o en el intervalo dt. El desplazamiento total es la suma de los infinitos desplazamientos infinitesimales entre los instantes t0 y t.
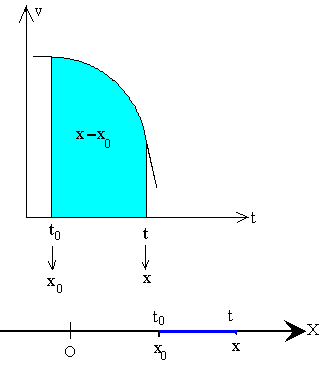 | En la figura, se muestra una gráfica de la velocidad en función del tiempo, el área en color azul mide el desplazamiento total del móvil entre los instantes t0 y t, el segmento en color azul marcado en la trayectoria recta.Hallamos la posición x del móvil en el instante t, sumando la posición inicial x0 al desplazamiento, calculado mediante la medida del área bajo la curva v-t o mediante cálculo de la integral definida en la fórmula anterior. |
Ejemplo:
Un cuerpo se mueve a lo largo de una línea recta de acuerdo a la ley v=t3-4t2 +5 m/s. Si en el instante t0=2 s. está situado en x0=4 m del origen. Calcular la posición x del móvil en cualquier instante.
Cuando se tiene la gráfica de una función continua resulta bastante fácil señalar en qué intervalo la función es creciente, decreciente o constante. Sin embargo, no resulta fácil decir en que intervalo la función es creciente, decreciente o constante sin la gráfica de la función.
El uso de la derivada de una función puede ayudar a determinar si una función es creciente, decreciente o constante en un intervalo dado. Para esto, se necesita el teorema y la definición a continuación para mostrar varios ejemplos.
Teorema: Sea f una función derivable en el intervalo (a,b). Luego,
i) Si f’(x)>0 para todo x en el intervalo abierto (a,b), f es creciente en (a,b).
ii) Si f’(x)<0 para todo x en el intervalo abierto (a,b), f es decreciente en (a,b).
iii) Si f’(x) = 0 para todo x en el intervalo abierto (a,b), f es constante en (a,b).
Definición: Si un número c está en el dominio de una función f, c se conoce como un número crítico (valor crítico) de f si f’(c) = 0 ó f’(c) no existe.
A continuación una guía para construir la gráfica de una función usando la derivada:
1) Halla f’(x) (la derivada de f).
2) Halla los números críticos, igualando f’(x) a cero y resolviendo para x. Incluir también todos los valores de x donde la derivada no existe (es decir, no está definida).
3) Evalúa cada número crítico c en la función f para obtener los puntos críticos.
4) Localiza los puntos hallados en el paso anterior (3) en el plano cartesiano.
5) Determina en qué intervalo la función es creciente, decreciente o constante, usando el signo de la derivada. (Es decir, usa el teorema).
6) Dibuja la gráfica, de manera que sea creciente en el intervalo donde la derivada es positiva, decreciente en el intervalo donde la derivada es negativa y horizontal en el intervalo donde la derivada es igual a cero.
Valores Extremos (Máximos y Mínimos Absolutos)
Si f es una función continua en el intervalo [a,b], entonces existe un número c en el intervalo [a,b] tal que f(c)>f(x) para todo x en el intervalo [a,b]. En este caso, f(c) se conoce como un valor máximo (o máximo absoluto) de f.
Si f(c) es el máximo de f en el intervalo [a,b] se dice que f alcanza su máximo en c, y en ese caso, el punto (c,f(c)) es el punto más alto de la gráfica.
Análogamente, si existe un número c en el intervalo [a,b] tal que f(c)<f(x) para todo x en el intervalo [a,b], entonces f(c) es un valor mínimo (o mínimo absoluto) de f.
Si f(c) es el mínimo de f en el intervalo [a,b] se dice que f alcanza su mínimo en c, y en ese caso, el punto (c,f(c)) es el punto más bajo de la gráfica.
A los valores máximos y mínimos de una función en un intervalo cerrado se les conoce como valores extremos o extremos de la función en el intervalo.
SEGUNDA DERIVADA
El Criterio o prueba de la segunda derivada es un teorema o método del calculo matemático en el que se utiliza la segunda derivada para efectuar una prueba simple correspondiente a los máximos y mínimos relativos.
Se basa en el hecho de que si la gráfica de una función  es convexa en un intervalo abierto que contiene a
es convexa en un intervalo abierto que contiene a  , y
, y  debe ser un mínimo relativo de
debe ser un mínimo relativo de . De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a
. De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a  y
y  debe ser un máximo relativo de
debe ser un máximo relativo de  .
.
Sea  es convexa en un intervalo abierto que contiene a
es convexa en un intervalo abierto que contiene a  , y
, y  debe ser un mínimo relativo de
debe ser un mínimo relativo de . De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a
. De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a  y
y  debe ser un máximo relativo de
debe ser un máximo relativo de  .
. una función tal que
una función tal que  y la segunda derivada de
y la segunda derivada de  existe en un intervalo abierto que contiene a
existe en un intervalo abierto que contiene a 
- Si
 , entonces
, entonces  tiene un máximo relativo en
tiene un máximo relativo en  .
. - Si
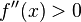 , entonces
, entonces  tiene un mínimo relativo en
tiene un mínimo relativo en  .
.
Si  , entonces el criterio falla. Esto es,
, entonces el criterio falla. Esto es,  quizás tenga un máximo relativo en
quizás tenga un máximo relativo en  , un mínimo relativo en
, un mínimo relativo en  o ninguno de los dos. Tomar como ejemplo la función f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada.
o ninguno de los dos. Tomar como ejemplo la función f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada.
 , entonces el criterio falla. Esto es,
, entonces el criterio falla. Esto es,  quizás tenga un máximo relativo en
quizás tenga un máximo relativo en  , un mínimo relativo en
, un mínimo relativo en  o ninguno de los dos. Tomar como ejemplo la función f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada.
o ninguno de los dos. Tomar como ejemplo la función f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada.PUNTO DE INFLEXIÓN Y CONCAVIDAD
Definición de concavidad:Se dice que la gráfica de una función f es cóncava hacia arriba en un intervalo A,
Note que es la función derivada  la que debe ser creciente o decreciente en el intervalo A.
la que debe ser creciente o decreciente en el intervalo A.
En la siguiente representación gráfica, una función f es cóncava hacia arriba en el intervalo![$]a,b[$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/aplicacionesderivada/html/img10.gif) y cóncava hacia abajo en el intervalo
y cóncava hacia abajo en el intervalo ![$]b,c[$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/aplicacionesderivada/html/img153.gif)
En la siguiente representación gráfica, una función f es cóncava hacia arriba en el intervalo
 |
 |
 |
BIBLIOGRAFIA:
http://es.wikipedia.org/wiki/Regla_de_la_cadena
http://facultad.bayamon.inter.edu/ntoro/aplic.htm
http://es.wikipedia.org/wiki/Criterio_de_la_segunda_derivada
https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/aplicacionesderivada/html/node5.html
.jpg)
.jpg)